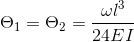EVENLY DISTRIBUTED LOAD SUPPORTED BEAM DEFLECTION CALCULATOR
|
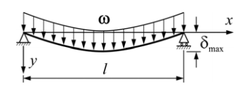
This equation can be used to calculate the maximum deflection in a beam supported at both ends, with an evenly distributed load along the length of the beam:
Where:
E = Youngs Modulus I = Second Moment of Area ω = Evenly Distributed Load l = Length of Beam ∂ = Maximum Deflection θ = Angle of Deflection (Scroll down to find Deflection Slope Angle calculator) |
Looking for maximum deflection angle? Scroll down to find a calculator for deflection slope angle.
|
Not sure what this Even Load Supported Beam Deflection Calculator is doing?
This beam deflection calculator is designed to calculate the deflection of a simply supported beam with a across the length of the beam. If this doesn't look like the arrangement you are trying to calculate go back to the beam deflection home page to select a more suitable calculator.
An explanation of the variables:
E = Young's Modulus - Young's Modulus is a property of the material defined and is calculated using the stress and strain. Typical Young's Modulus values for materials can be found here.
I = Second Moment of Area - second moment of area, or moment of inertia is a product of the beams cross section and its ability to resist bending.
ω = Evenly distributed load - This is the mass or weight acting on the beam, in this case spread across the whole beam uniformly.
l = Length of beam - length of the beam from the first fixed point to the second fixed point.
∂ = Deflection - This is the maximum physical displacement of the middle point as a result of the load and properties of the beam.
θ = Angle of Deflection - this is the final angle of each end of the beam in its deflected position, relative the the previous, horizontal position.
We then plumb in all the information you give us into the equation above, and spit out the deflection! The great news is you don't have to worry about converting units! The deflection calculator will do that for you.
An explanation of the variables:
E = Young's Modulus - Young's Modulus is a property of the material defined and is calculated using the stress and strain. Typical Young's Modulus values for materials can be found here.
I = Second Moment of Area - second moment of area, or moment of inertia is a product of the beams cross section and its ability to resist bending.
ω = Evenly distributed load - This is the mass or weight acting on the beam, in this case spread across the whole beam uniformly.
l = Length of beam - length of the beam from the first fixed point to the second fixed point.
∂ = Deflection - This is the maximum physical displacement of the middle point as a result of the load and properties of the beam.
θ = Angle of Deflection - this is the final angle of each end of the beam in its deflected position, relative the the previous, horizontal position.
We then plumb in all the information you give us into the equation above, and spit out the deflection! The great news is you don't have to worry about converting units! The deflection calculator will do that for you.