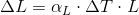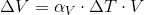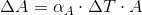THERMAL EXPANSION CALCULATOR

Thermal expansion is normally calculated in two ways, as a linear (single dimension) or volumetric (3 dimensional) measurement. Depending on the case, each method is useful, as finding out how a beam would extend due to heat would only require a linear method, however when trying to find out how a body of liquid expands with temperature, volumetric might be best.

Linear Thermal Expansion Calculator

Linear Thermal Expansion is calculated using the following formula:

Linear thermal expansion formula: Change in length = coefficient of linear thermal expansion x change in temperature x initial length

Where:
L = Initial Length
ΔL = The change in Length
αL = Coefficient of Linear Thermal Expansion
ΔT = Change in temperature

This thermal expansion calculator uses the most common formula used to estimate the expansion caused by a change in temperature. The linear thermal expansion equation calculates the increase or decrease in a single dimension of a body as a result of a change in temperature, it is calculated by multiplying the dimension of the material by the Coefficient of Linear Thermal Expansion for that material. The Coefficient of Linear Thermal Expansion, or CLTE, is commonly displayed as a product of a length/length per temperature unit. As this is the case, the unit of length does not matter provided both units of length are the same. Once you have your coefficient, you need the length of the expansion to be measured, and the temperature range for the scenario, put it all into the calculator and go!

Volumetric Thermal Expansion Calculator

Volumetric Thermal Expansion is calculated using the following formula:

Volumetric thermal expansion formula: Change in volume = coefficient of volume thermal expansion x change in temperature x initial volume

Where:
V = Initial Volume
ΔV = The change in Volume
αV = Coefficient of Volumetric Thermal Expansion

Volumetric Thermal Expansion is calculated in a very similar fashion to Linear expansion, only with measurements of volume, not length! Coefficients of Volumetric Expansion are proportional to Linear coefficients, being triple the value of linear expansion, so its easy to convert from one to the other if you cant find the correct coefficient.

Area Thermal Expansion

Area Thermal Expansion is calculated using the following formula:

Where:
A = Initial Area
ΔA = The change in Area
αA = Coefficient of Area Thermal Expansion

As with linear it Area Expansion is calculated the same way as above, normally double that of linear expansion.

Table Of Thermal Expansion Coefficients

Thermal Expansion of Common Materials
Material	Coefficient of thermal expansion (CTE)		Reference
Material	Linear Expansion (X10^-6 K^-1)	Volume Expansion (X10^-6 K^-1)	Reference
Low Carbon Steel	10.1 - 14.9	30.3 - 44.7	Matweb
High Carbon Steel	9.9 - 14.8	29.7 - 44.4	Matweb
Stainless Steel (316)	18.5	55.5	Matweb
Aluminium (pure)	23.6	70.8	Chicago University
Water (293 Kelvin)	69	207	efunda
Water (277 Kelvin)	0	0	University of Oregon
Copper	16.4	49.2	Matweb
Brass	18 - 26	54 - 78	Matweb
ABS	60 - 100	180 - 300	Roechling

Important Notes for Thermal Expansion Calculations!

Its important to remember when using thermal expansion coefficients, figures quoted are normally at 20°C, its important to know the coefficients vary with temperature! for example, thermal expansion of water is a curve, with centre at approximately 4°C. At this point, the thermal expansion is zero, however either side the expansion coefficient increases. In most cases, the difference is very small, but worth checking, especially near the melting point of the material.

Thermal Expansion Examples

Linear Thermal Expansion Example

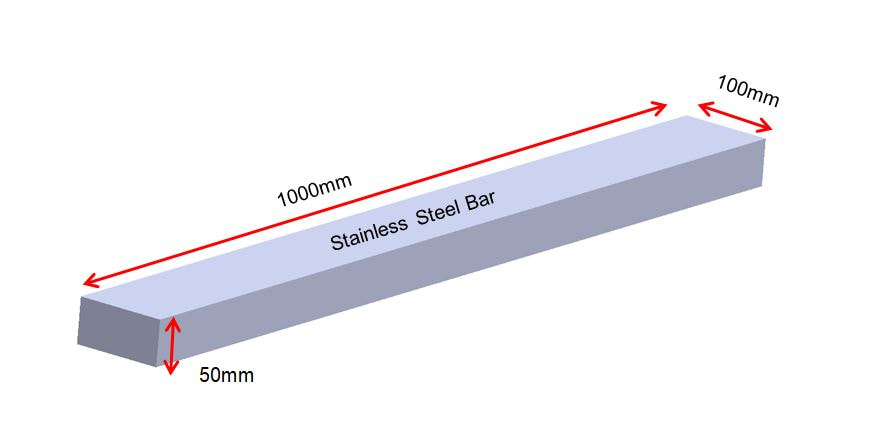
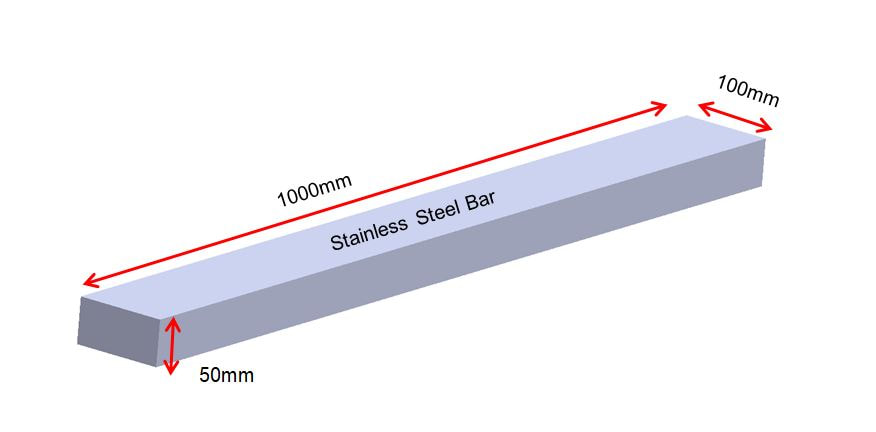
In this example, we take a stainless steel bar 1000mm long, 100mm wide and 50mm thick. If we heat the bar from 20°C to 300°C, we can calculate the amount the bar will expand in each direction using the linear thermal expansion calculator.
If:
L = 1000mm
αL = 18.5 X 10^-6 K^-1, or 0.0000185mm/mm°C
ΔT = 300-20 = 280°C

Stainless Steel Bar Thermal Expansion example

By multiplying our three variables according the the linear thermal expansion equation, we can find that the bar will expand by approximately 5.2mm, bringing the overall length to 1005.2mm.

Volumetric Thermal Expansion Example

Using the same example, a stainless steel bar 1000mm long, 100mm wide and 50mm thick heated to 300°C, we can calculate the amount the volume of the bar will change using the volumetric thermal expansion calculator.
If:
L = 1000mm
W = 100mm
D = 50mm
αV = 55.5 X 10^-6 K^-1, or 0.0000185mm/mm°C
ΔT = 300-20 = 280°C

First we need to find the Volume:
V = L x W x D = 5,000,000mm^3

Using the calculator above, we can calculate that the Volume of the bar will expand by 77,000 cubic millimetres, bringing the volume to 5,077,000 cubic millimetres.