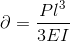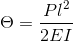SINGLE LOAD CANTILEVER DEFLECTION CALCULATOR
|
This equation can be used to calculate the maximum deflection in a beam supported at one end:
Where:
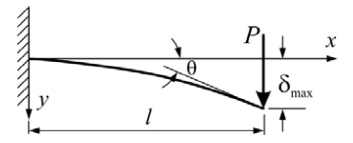
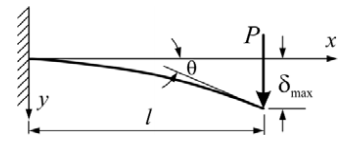
E = Youngs Modulus I = Second Moment of Area P = Point Load l = Length of Cantilever ∂ = Deflection θ = Angle of Deflection (Scroll down to find Deflection Slope Angle) |
Looking for maximum deflection angle? Scroll down to find the deflection slope angle.
|
Not sure what this Beam Deflection Calculator is doing?
This beam deflection calculator is designed to calculate the deflection of a simply supported cantilever with a single load point at one end. If this doesn't look like the arrangement you are trying to calculate go back to the beam deflection home page to select a more suitable calculator.
An explanation of the variables:
E = Young's Modulus - Young's Modulus is a property of the material defined and is calculated using the stress and strain. Typical Young's Modulus values for materials can be found here.
I = Second Moment of Area - second moment of area, or moment of inertia is a product of the beams cross section and its ability to resist bending.
P = Point Load - This is the mass or weight acting on the beam, in this case at the furthest point from fixed end.
l = Length of Cantilever - length of the beam from the fixed point to the end of the beam, and in this case, also the point load.
∂ = Deflection - This is the maximum physical displacement of the end point as a result of the load and properties of the beam.
θ = Angle of Deflection - this is the final angle of the beam in its deflected position.
We then plumb in all the information you give us into the equation above, and spit out the deflection! The great news is you don't have to worry about converting units! The deflection calculator will do that for you.
An explanation of the variables:
E = Young's Modulus - Young's Modulus is a property of the material defined and is calculated using the stress and strain. Typical Young's Modulus values for materials can be found here.
I = Second Moment of Area - second moment of area, or moment of inertia is a product of the beams cross section and its ability to resist bending.
P = Point Load - This is the mass or weight acting on the beam, in this case at the furthest point from fixed end.
l = Length of Cantilever - length of the beam from the fixed point to the end of the beam, and in this case, also the point load.
∂ = Deflection - This is the maximum physical displacement of the end point as a result of the load and properties of the beam.
θ = Angle of Deflection - this is the final angle of the beam in its deflected position.
We then plumb in all the information you give us into the equation above, and spit out the deflection! The great news is you don't have to worry about converting units! The deflection calculator will do that for you.